Ternary search is an inductive approach using the decrease and conquer technique to locate the element in the data structure.
This approach is similar to binary search however, instead of dividing the search range into two parts we divide it into three parts resulting in two midpoint values. The main distinction between binary and ternary search is the time complexity, as ternary outperforms binary with a time complexity of O(log n base 3) in comparison to O(log n base 2) of binary search.
RCTerChecker determines the rank from which all ranks need to be removed from rank 0, in contrast to iterating from the top towards the lower ranks in the naive implementation of the RationalClosure.
This is an amended version of the RCTerChecker that allows the user to enter multiple queries in one instance, whereas the RCTerChecker only allows one query at a time.
This divide and conquer approach uses the fork/join framework. The framework uses ForkJoinPool, which manages a pool of worker threads. The framework "forks" that is recursively splits the program into smaller independent subtasks that run asynchronously. After which, the "join" is called which recursively joins into a single result.
In this implementation, the negations of the antecedents along with the rank at which the antecedents become consistent with the knowledge base are stored in a hashmap.
Java 16.0.2 
TweetyProject library 1.20 
Apache Maven 3.8.6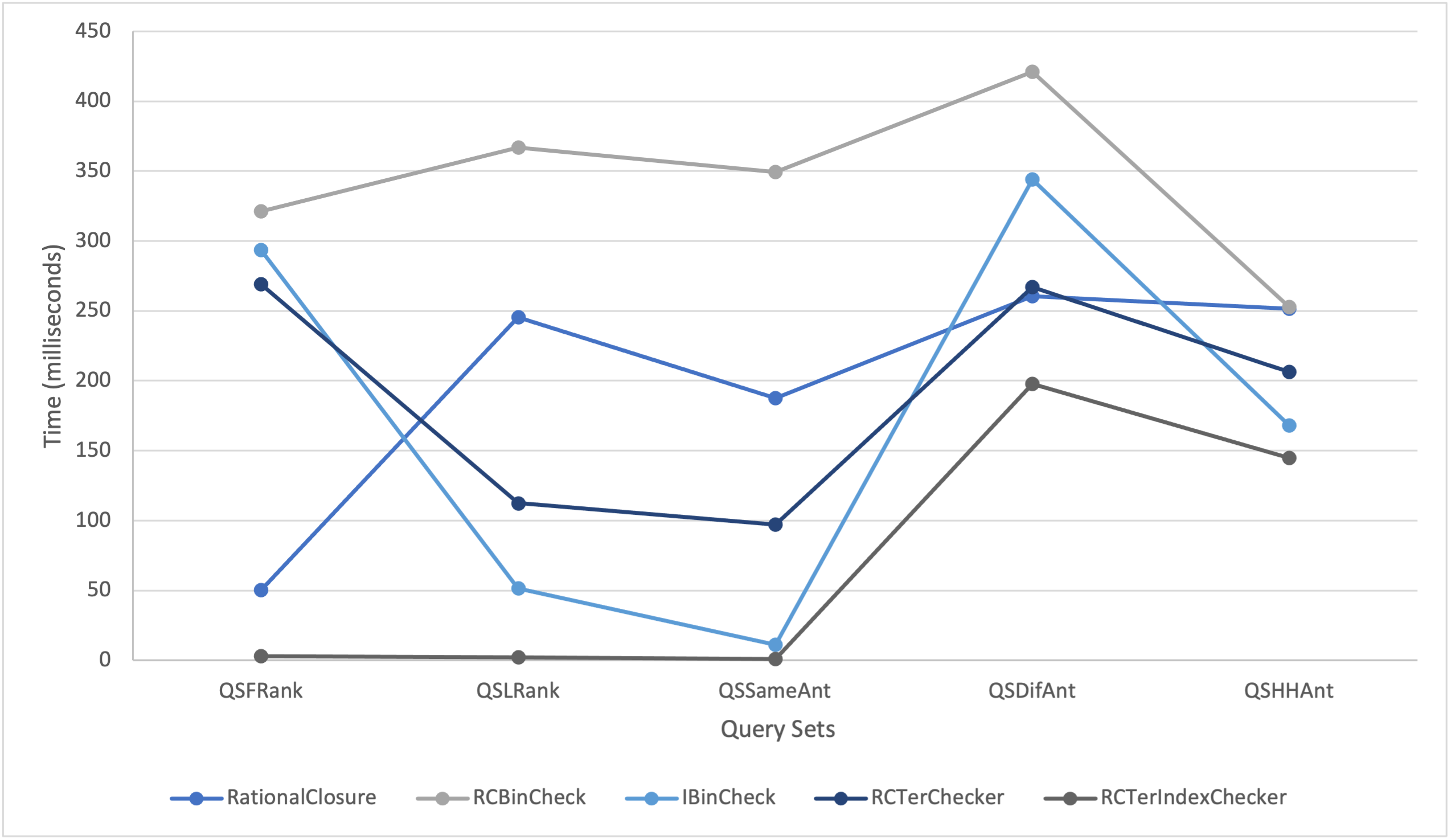 
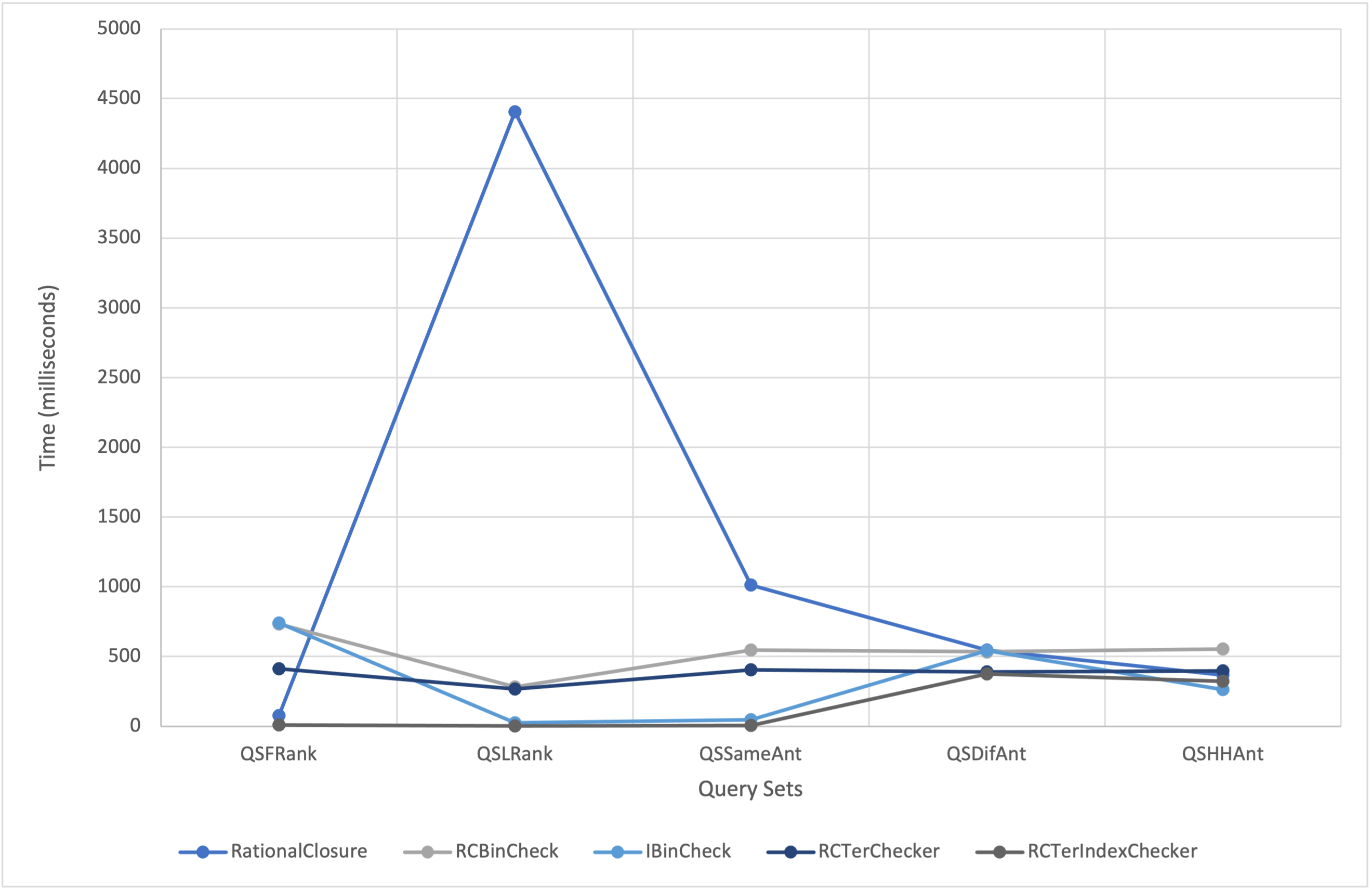
The reasoners are fully functional console-applications, each with their own specifications to test scalability. The first optimization allows the user to enter one query at a time whereas the second reasoner allows the user to enter multiple queries at a time. This allowed us to investigate the impact of scalability on computational speedup. The results of the tests indicate that the RCTerChecker performs significantly faster than the RCBinCheck when the rank at which the antecedent becomes consistent with the knowledge base is the final rank. We can deduce that because the ternary approach has two midpoint values instead of the single midpoint value of the binary search, it is able to find the rank more quickly due to the search range being split into three parts instead of two. That being said the ternary approach favours antecedents that become consistent at ranks with a higher number as opposed to the binary search.
The extent to which the RCTerIndexChecker outperforms the IBinCheck for all query sets tends to increase as the number of ranks in the knowledge base decreases. However, in some cases the IBinCheck outperforms the RCTerIndexChecker for instances of half repeated and half unique antecedents. Overall, the performance of the RCTerIndexChecker was fairly uniform for each query set, which disproves the theory that the number of ranks in a knowledge base is a major factor in whether or not the optimization will perform better. Instead, it suggests that the variable of interest is the ranks at which the antecedents of the queries become consistent with the knowledge base.
