Theory

Attributive Language with Class Complements -Description Logics
ALC DL is a decidable subset of First Order Logic
Introduction
An Ontology is a machine-readable representation of things, groups of things, and relationships between things.
ALC DL formalises ontologies as follows:
- Things are referred to as instances
- Groups of things are referred to as classes
- Relationships between things are referred to as relations
- Negation of elements in the domain
- Conjunction and Disjunction of elements in the domain
- Quialifiers: Universal restrictions and Existential Restrictions
- Domain hierarchies (i.e. subclasses)
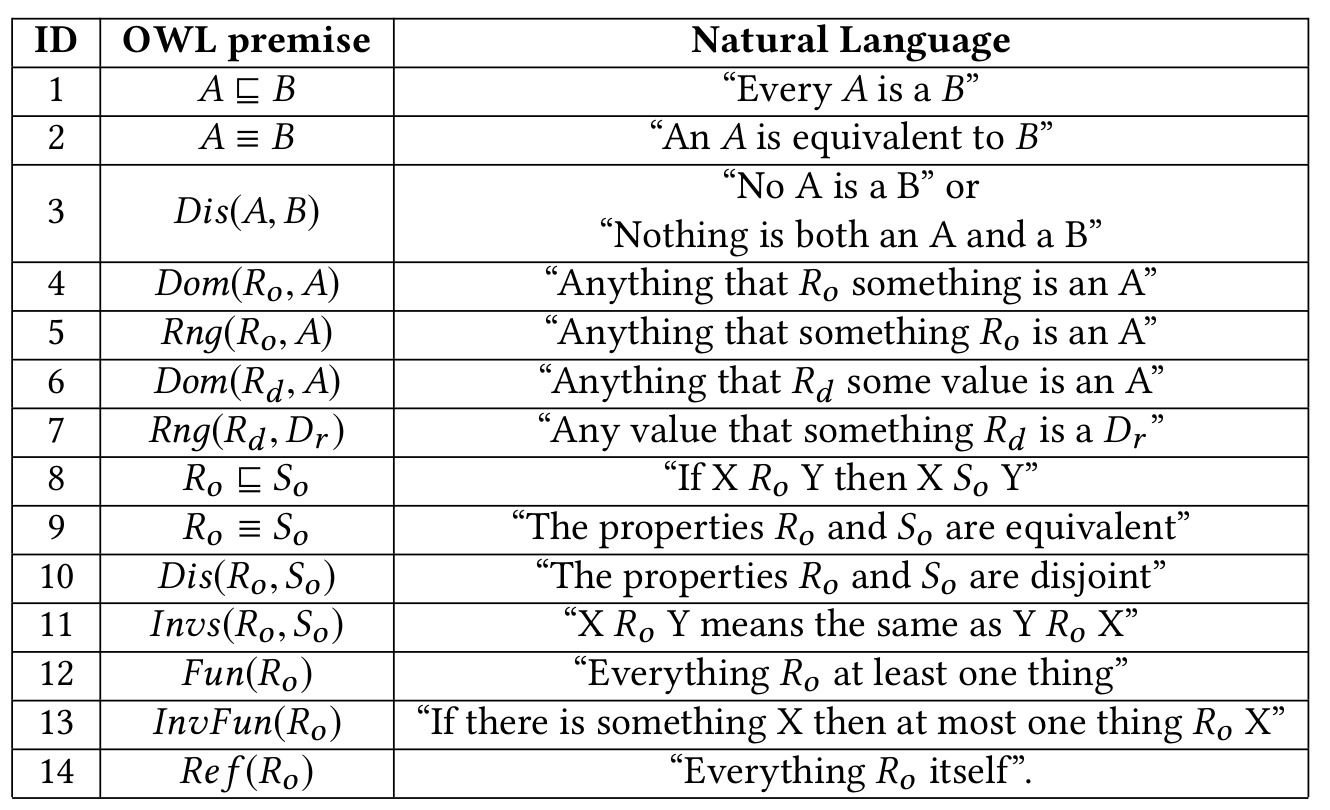
Syntax
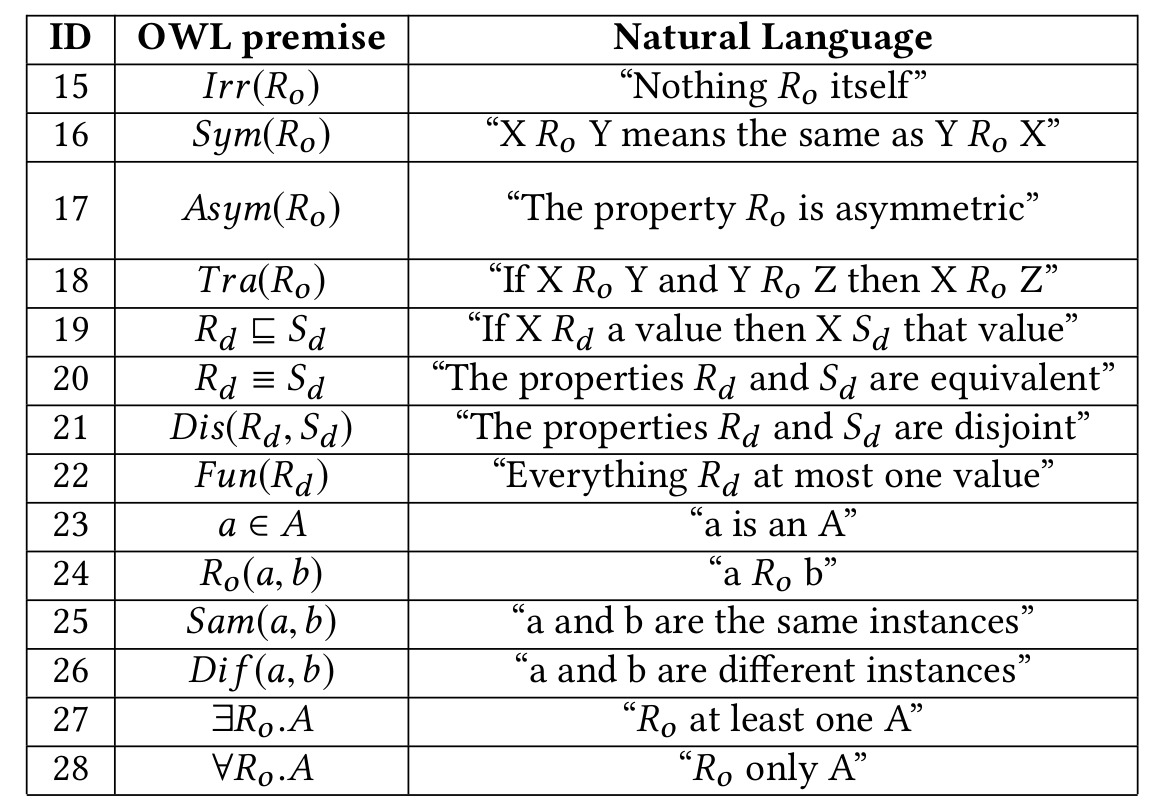
| Symbol | Description | Example | Read |
|---|---|---|---|
| ⊤ is a special concept with every individual as an instance | top | ||
| empty concept | bottom | ||
| intersection or conjunction of concepts | C and D | ||
| union or disjunction of concepts | C or D | ||
| negation or complement of concepts | not C | ||
| universal restriction | all R-successors are in C | ||
| existential restriction | an R-successor exists in C | ||
| Concept inclusion | all C are D | ||
| Concept equivalence | C is equivalent to D | ||
| Concept definition | C is defined to be equal to D | ||
| Concept assertion | a is a C | ||
| Role assertion | a is R-related to b |
Generating Single Justifications
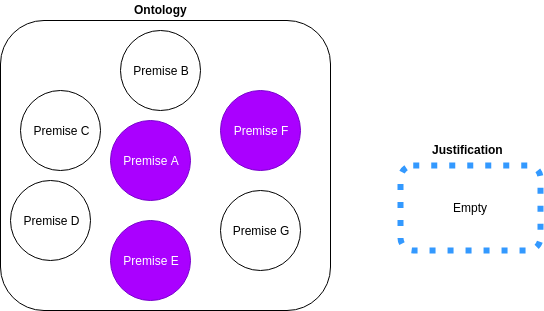
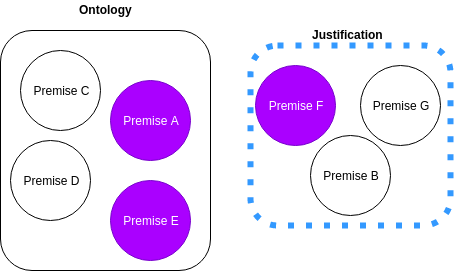
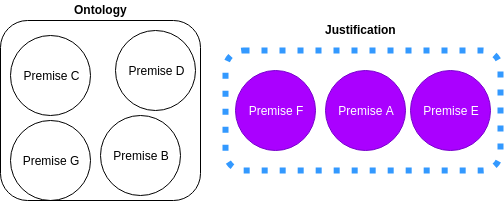
A justification is a minimal set of premises that are required to be true in order for an entailment to hold.
Algorithm
expansion phase
-
Determine if the ontology O is empty
- if O is empty, then the justification is an empty set.
-
Else, for each premise i in O:
- Add i to J
- Test if J entails the Conclusion, if so, go to the contraction phase
contraction phase
-
For each premise i in J:
- if J without i entails the conclusion, then remove i from J.
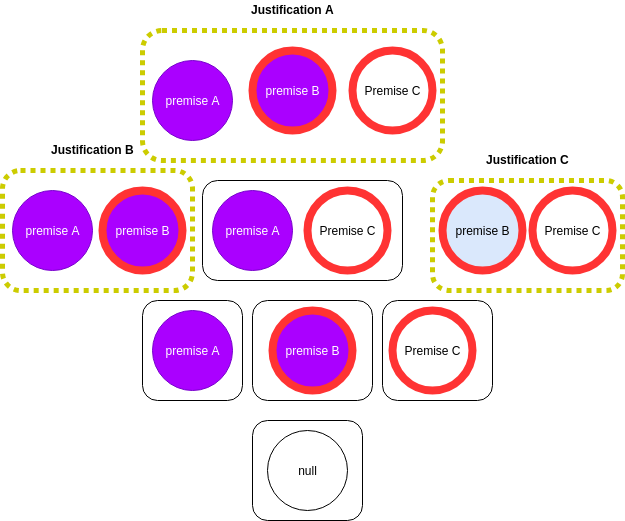
Generating All Justifications
The necessity of multiple justifications for an entailment η stems from the need to aid the understanding of domain experts when they debug an ontology. This may be induced by the need for an alternative justification for an entailment, which ultimately produces a different explanation for the same entailment η.
Algorithm (brute-force)
- We start by computing the power set of the ontology O and set it to S.
- We then test each element ι ∈ S for justifications of η.
- Then we create a new set J′ = {ι|∀ι ∈ S, ι |= η}.
- We then remove all duplicate justifications in J′.
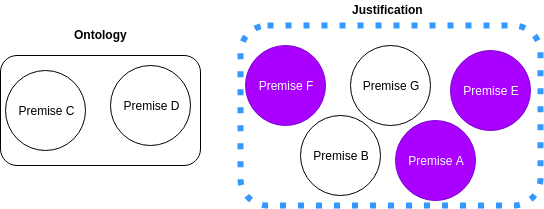
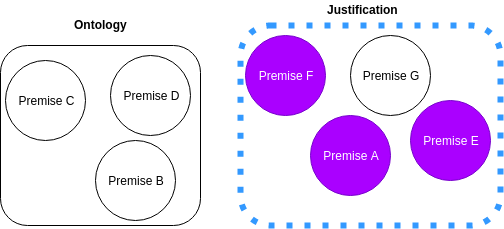
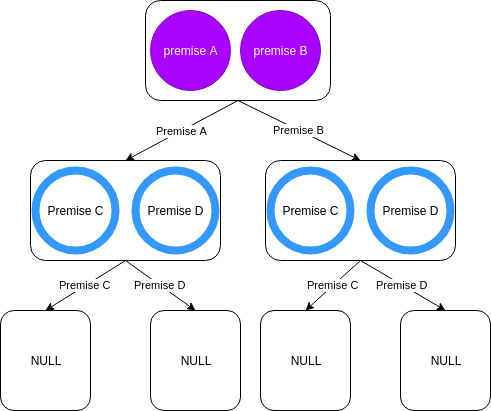
Reiter’s Hitting Set Tree
We denote intermediate nodes with v and successor nodes v′, which are connected to v by an edge with a premise α such that α is in the justification contained in v but not in the justification contained in v′ . When v ′ ≡ ∅, then it is a leaf node. Furthermore, for any node v′′, the set of premises that are in the path from the root to the node v′′ do not intersect with the justification in v′′.- We begin by choosing a premise α ∈ v which is not in the edges of the children of node v.
- We then let S be the disjunction of the chosen premises {α} and the set of premises found in the path traced from v to the root node of the tree. Then we set O ′ ← O\S.
- We test if the new ontology O ′ entails η . If that is the case, we compute a justification J for η using the new ontology O ′ . Whereas if the new ontologyO ′ does not entail η, we set the justification J = ∅
- We then make a new node v ′ and set its justification to be J
- We add an edge e between v and v ′ , and we label e with the premise α
- We reinsert all the premises in S back into O.
Generating Proof Trees
A justification is analogous to a set of axioms for a theorem. This means that an explanation for the pertinent conclusion needs to be computed by forming new propositions that are entailed within the justification.
Introduction
We define an explanation Σ(η) of an entailment η to be apair (J , {ε_1 , ε_2 , ε_3 , ..., ε_n }), where J is a justification for an entailment η and {ε_1 , ε_2 , ε_3 , ..., ε_n } is a minimal set of intermediate entailments that link the justification J to the entailment η. The minimality of {ε_1 , ε_2 , ε_3 , ..., ε_n } implies that if an entailment β ∈ {ε_1 , ε_2 , ε_3 , ..., ε_n } is removed then {ε_1 , ε_2 , ε_3 , ..., ε_n }\β cannot logically link η with J.
Lemmatization
Suppose we have an ontology O from which we derive a justification J for an entailment η whereby O entails η. The goal is to lemmatise J into J′ such that J′ is “less complex” than J.
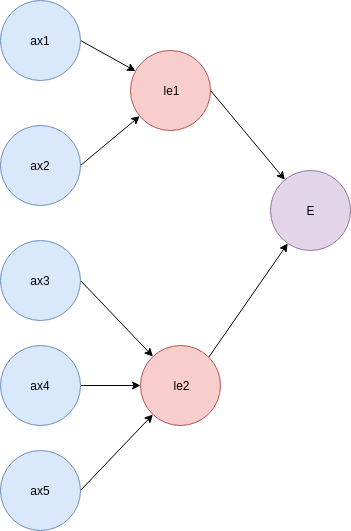
Proof Tree Generation
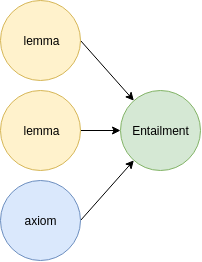
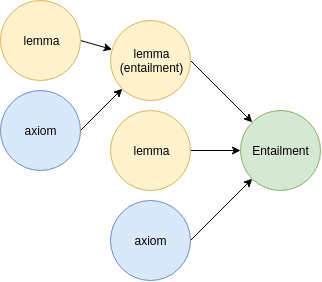
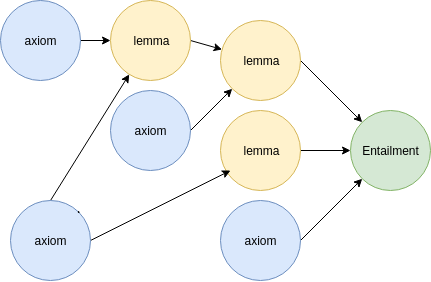
The above figure illustrates what a construction of an explanation for an entailment E looks like. In this case, η = E, J = {ax1, ax2, ax3, ax4, ax5}, and {ε_1 , ε_2 , ε_3 , ..., ε_n } = {le1, le2}. We observe that {ax1, ax2} |= le1, {ax3, ax4, ax5} entails le2, and {le1, le2} entails E. Without le1 and/or le2, it cannot be proven that η entails E.
Example input-
The first step is to lemmatise J to give a new lemmatised justification ζ.
- We then create an initial proof tree Σ using ζ.
- We check if ζ contains leaf nodes with premises that can be lemmatised.
If so:-
We choose a lemma α in our proof tree Σ that can be lemmatised. We compute a justification β for α using J
- We then lemmatise β in order to generate a new justification γ
- We insert γ to the proof tree Σ.
After this, we return to step 3.- At this point, the construction of the proof tree is now completed
Proposition Translation
For each and every node in the proof tree, we employ a parse tree which converts an ALC DL proposition into an equivalent English proposition.
Explanation Generation
An complete explanation is generated by traversing a proof tree in a pre-order fashion. Whenever we encounter a node, we print the contents of the node (i.e. English proposition) as a statement and we indicate that this statement is implied because of the children of the pertinent node.
-
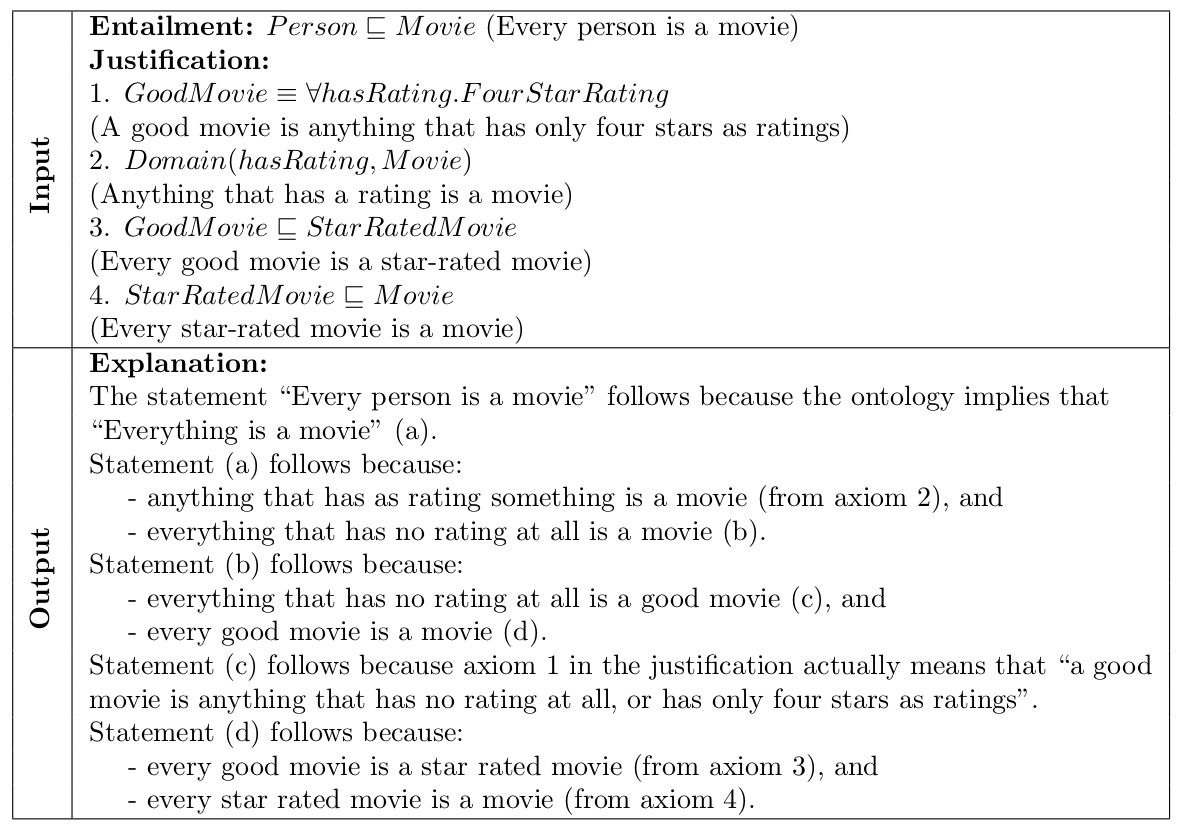 Example taken from Matthew Horridge's "Justification-based explanation in ontologies." (2011).
Example taken from Matthew Horridge's "Justification-based explanation in ontologies." (2011).
Get in touch
Contact us if you have any questions
-
-